Electromagnetic wave propagation

Plane waves are a well-known solution to Maxwell's equations in a non-conducting, source-free, anisotropic linear dielectric medium

\[ \nabla \times \nabla \times {\bf E} = -\mu {\boldsymbol \epsilon} \frac{\partial^2 {\bf E}}{\partial t^2}, \]

where ${\bf E}$ is the electric field, ${\boldsymbol \epsilon}$ is the bulk dielectric permittivity tensor, and $\mu$ the bulk isotropic permeability of the medium. Substituting ${\bf E}$ for the plane wave solution, ${\bf E} = {\bf E}_0 \exp[i({\bf k}\cdot {\bf x} - \omega t)]$, the problem reduces to

\[ ({\bf K} + \omega^2 \mu {\boldsymbol \epsilon}) \cdot {\bf E} = {\bf 0}, \]

where ${\bf K} = {\bf k}\times{\bf k} \times$ is the matrix representation of the twice-applied cross product. The above equation implies that $\det( {\bf K} + \omega^2 \mu {\boldsymbol \epsilon} ) = 0$. Hence, the eigenvalues and eigenvectors of the normalized Christoffel tensor ${\boldsymbol \epsilon}^{-1} {\bf K}/(\mu k^2)$ are the permitted wave velocities squared $V^2 = {\omega^2}/{k^2}$ and wave polarization, respectively.

Homogenization

If wave lengths are much longer than the average grain size, the problem can be closed by approximating the bulk polycrystalline permittivity tensor by the grain-averaged permittivity tensor

\[{\boldsymbol \epsilon} = \langle {\boldsymbol \epsilon}' \rangle,\]

constructed by averaging over all grain orientations (over the CPO).

Glacier ice

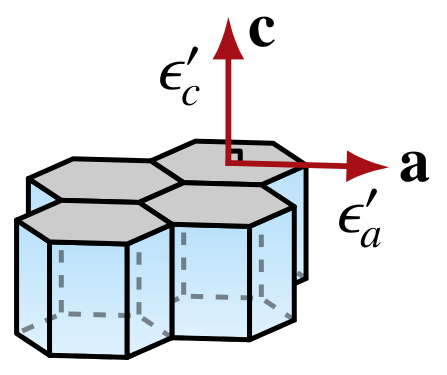
If ice grains are approximated as transversely isotropic w.r.t. the $c$-axis, the dielectric permittivity tensor of a single crystal can be written as $$ {\boldsymbol \epsilon}' = (2\epsilon_{a}' + \epsilon_{c}') \frac{\bf I}{3} + (\epsilon_{c}'-\epsilon_{a}') \left( {\bf c}^2 - \frac{\bf I}{3} \right), $$ where $\epsilon_{c}'$ and $\epsilon_{a}'$ are the permittivities parallel and perpendicular to the $c$ axis. In this case, the grain-averaged permitivity is simply

\[ \langle {\boldsymbol \epsilon}'\rangle = (2\epsilon_{a}' + \epsilon_{c}') \frac{\bf I}{3} + (\epsilon_{c}'-\epsilon_{a}') \left( \langle {\bf c}^2 \rangle - \frac{\bf I}{3} \right) , \]

where $\langle {\bf c}^2 \rangle$ is the second-order structure tensor.

Travel time difference

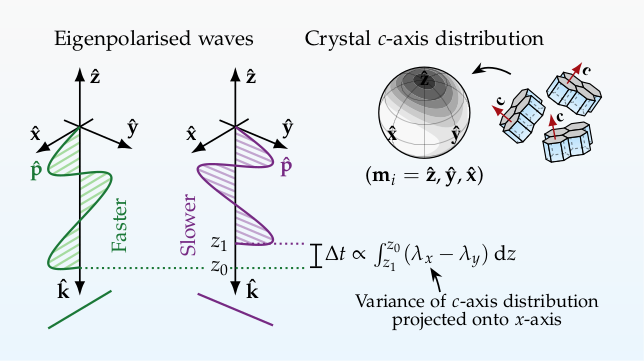
Radioglaciological field surveys are a popular approach for understanding the depth-averaged CPOs of ice sheets and glaciers. Such surveys rely on the fact that orthogonally polarized radio waves travel at different speeds depending on the misalignment between wave polarization and the CPO principal axes (birefringence). Thus, if travel-time delays can be measured accurately for orthogonally polarized waves, inferences about the CPOs of glaciers and ice sheets can be made.

To realize how, consider a frame where the CPO principal axes are aligned with the Cartesian coordinate system so that $\langle {\bf c}^2 \rangle = \operatorname{diag}(\lambda_x,\lambda_y,\lambda_z)$. It can be shown that two S-wave solutions exist for the above eigenvalue problem that have the distinct slownesses (inverse velocities) $$ S_i^2 = S_a^2 + \lambda_i \Delta S^2 $$ when (eigen)polarized along the ${\bf x}$- and ${\bf y}$-axis ($i=x,y$). Here, $S_c=\mu\epsilon'_c$ and $S_a=\mu\epsilon'_a$ are the monocrystal slownesses for waves polarized along the ${\bf c}$ and ${\bf a}$ axes of a single crystal, and $\Delta S=S^2_c - S^2_a$ is the squared monocrystal slowness anisotropy.

For a depth-varying fabric where $\lambda_i=\lambda_i(z)$, the two-way travel time difference between eigenpolarized waves, propagating from the surface at height $z=H$ down to $z=z_0$, and back, is

$$ \Delta t = t_x - t_y = 2 \int_H^{z_0} S_x(z) \,\mathrm{d}{z} - 2\int_H^{z_0} S_y(z) \,\mathrm{d}{z} . $$ Expanding the depth-depedent slowness $$ S_i(z) = \sqrt{S_a^2 + \lambda_i(z) \Delta S^2 } $$ around the isotropic state $\lambda_i=1/3$, it can be shown that $\Delta t$ is to first order $$ \Delta t \simeq \frac{\Delta S^2}{S_{\mathrm{iso}}} \int_H^{z_0} (\lambda_x-\lambda_y) \,\mathrm{d}{z}, $$ where $S_{\mathrm{iso}}=\sqrt{\mu(2\epsilon'_a+\epsilon'_c)/3}$ is the slowness within an isotropic polycrystal.

Thus, the travel time difference between vertically-propagating eigenpolarized waves is (approximately) proportional to the depth-integrated difference in horizontal eigenvalues.

📝 Code example

A code example is given below of how to calculate EM wave velocities using specfab. Notice that the problem depends on the relative permitivity and permeability, and that wave propagation is sensitive only the the lowest-order (coarsets degree) of CPO anisotropy, $\langle {\bf c}^2 \rangle$.

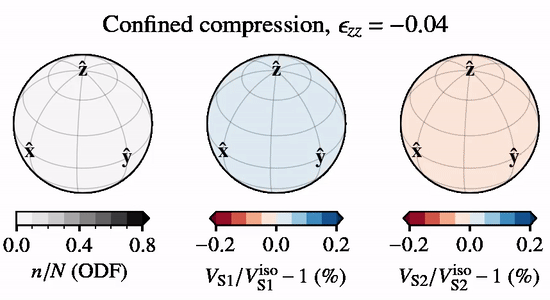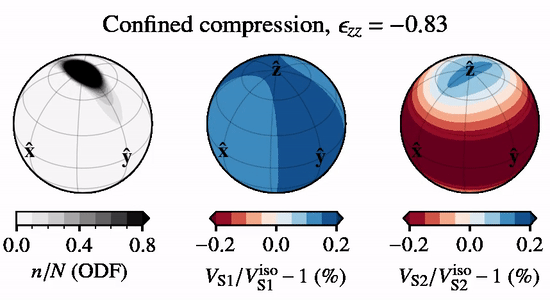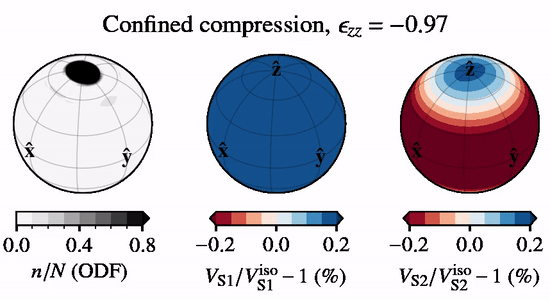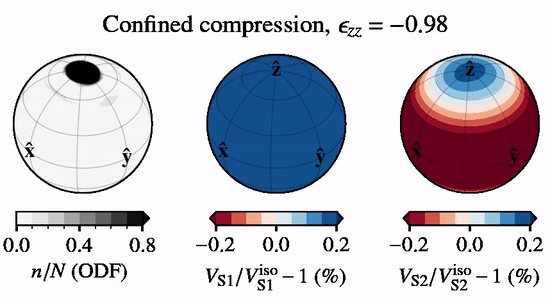
The animation to the right shows directional S-wave velocities for a CPO evolving under $xz$ confined compression, relative to an isotropic CPO, when subject to lattice rotation.

import numpy as np
from specfabpy import specfab as sf
lm, nlm_len = sf.init(4)
nlm = np.zeros((nlm_len), dtype=np.complex64) # state vector (array of expansion coefficients)

### Physical parameters (note eps=eps0*epsr, mu=mu0*mur)
epsr_c = 3.17        # relative permittivity of a single grain parallel to symmetry axis (c) 
epsr_a = 3.17-0.034  # relative permittivity of a single grain perpendicular to symmetry axis (a)
mur = 1              # relative permeability of a single grain

### CPO from second-order structure tensor
p = np.array([0,0,1]) # preferred c-axis direction
a2 = np.einsum('i,j', p,p) # = deltafunc(r-p) 
nlm[:sf.L2len] = sf.a2_to_nlm(a2) # l<=2 expansion coefficients

### Propagation directions of interest
theta, phi = np.deg2rad([0,90,]), np.deg2rad([0,0,]) # theta=colatitude, phi=longitude

### Calculate phase velocities
Vi = sf.Vi_electromagnetic_tranisotropic(nlm, epsr_c, epsr_a, mur, theta,phi) # fast and slow phase velocities are V_S1=vi[0,:], V_S2=vi[1,:]