Discontinous dynamic recrystallization (DDRX)
Following Placidi and others (2010), DDRX is modeled as a spontaneous mass decay—production process in orientation space \(S^2\), intended to represent the combined effect of nucleation and grain boundary migration. That is, mass is spontaneously exchanged between grains with different orientations depending on the local stress state, strain rate, and temperature, in a statistical sense.
The decay—production rate is defined as
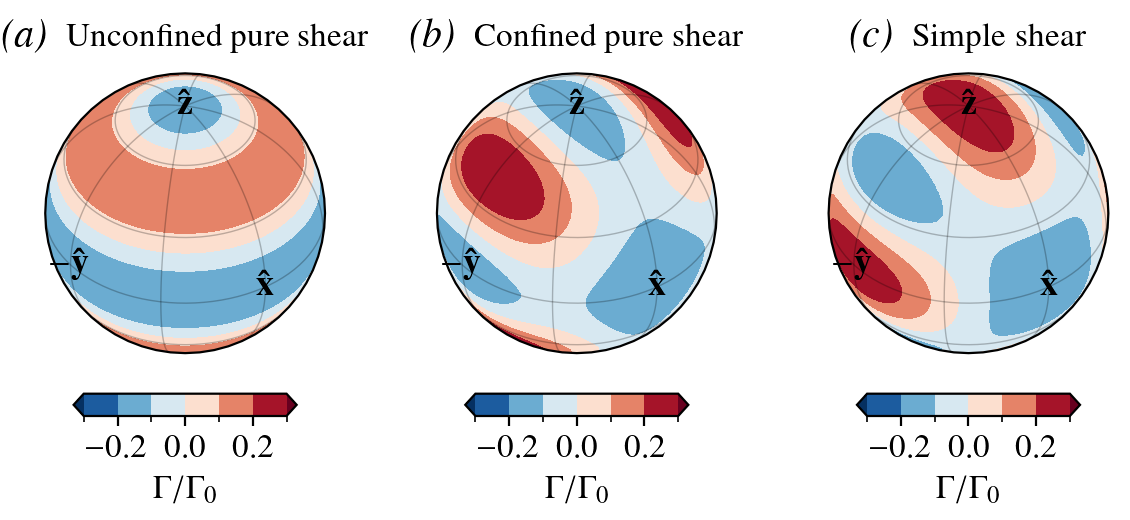
where the prefactor \(\Gamma_0\) accounts for the preferential (Arrhenius) activation at warm temperatures and the effect of strain-rate magnitude, defined as \begin{align} \Gamma_0 = \sqrt{\frac{{\dot{\boldsymbol\epsilon}}:{\dot{\boldsymbol\epsilon}}}{2}} A_{\Gamma}\exp(-Q_{\Gamma}/RT) . \end{align} Here, \({\dot{\boldsymbol\epsilon}}\) is the strain-rate tensor, \(R\) is the gas constant, \(T\) is the temperature, and \(A_{\Gamma}\) and \(Q_{\Gamma}\) have been calibration by Richards et al. (2021) and Lilien et al. (2023).
The deformability \(D\) is the square of the basal-plane resolved shear stress
relative to the average value of an isotropic fabric:
where \({\bf n}\) is an arbitrary slip-plane normal (\(c\)-axis for ice). Because \(D\) is largest for grains with an orientation favorable to easy glide, mass is spontaneously created/added to grains with such preferred orientations (in a statistical sense). Conversely, mass spontaneously decays if \(D<{\langle} D {\rangle}\), corresponding to grains with an unfavorable orientation being consumed by grains with a more favorable orientation to basal glide. Here, \({\langle} D {\rangle}\) is the grain-average deformability of the polycrystal, and the total mass of the polycrystal is conserved since \(\Gamma\) is zero on average, \(\langle\Gamma\rangle=\Gamma_0\langle D-\langle D\rangle\rangle=0\) (equal amounts of grain mass are created and destroyed per time).
The primary driver for grain boundary migration is generally regarded to be the contrast in dislocation density (stored strain energy) between grains. In this sense, \(1/D\) can be understood as a parameterization of the dislocation density: the larger \(1/D\) is, the more dislocations a grain has, and the more likely it is to be consumed (decay).
Nonlinear process
Since average deformability \(\langle D\rangle\) depends on the instantaneous CPO state — specifically, the structure tensors \(\langle{\bf c}^2\rangle\) and \(\langle{\bf c}^4\rangle\) — this crystal process is nonlinear (renders a nonlinear matrix problem below).
Limited use
Notice that this model is currently only relevant to slip-system normals. The model is therefore not yet useful for e.g. olivine.
Glacier ice
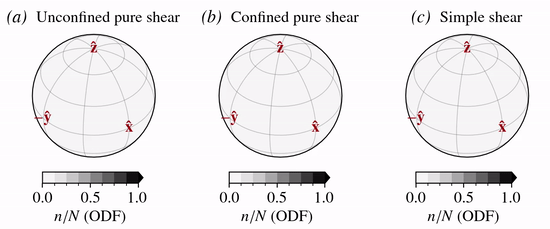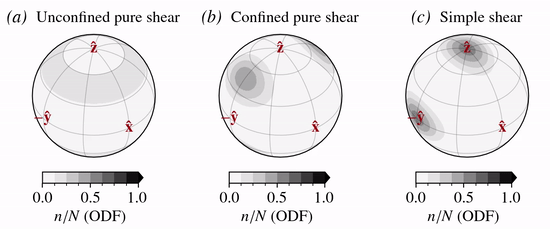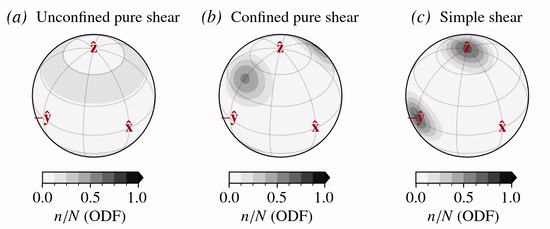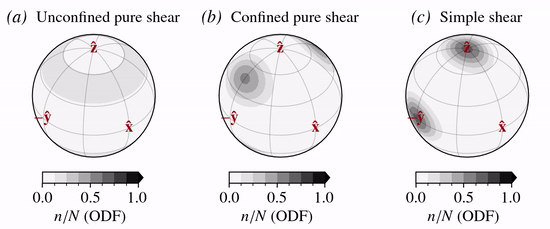
The normalized decay—production rate is shown below for three different stress states:

Matrix model
The corresponding effect on the continuous distribution function is
where \({\bf M_{\mathrm{DDRX}}}\) is given analytically in Rathmann and Lilien (2021).
Code example
import numpy as np
from specfabpy import specfab as sf
# L=8 truncation is sufficient in this case, but larger L allows a very strong fabric to
# develop and minimizes the effect that regularization has on low wavenumber modes (l=2,4)
lm, nlm_len = sf.init(8)
### Stress tensor experienced by parcel
S = np.diag([0.5, 0.5, -1.0]) # uniaxial compression along z-axis
### Numerics
Nt = 25 # number of time steps
dt = 0.05 # time-step size
### Initial fabric state
nlm = np.zeros((Nt,nlm_len), dtype=np.complex64) # n state vector
nlm[0,0] = 1/np.sqrt(4*np.pi) # normalized isotropic state at t=0
### Euler integration
for tt in np.arange(1,Nt):
nlm_prev = nlm[tt-1,:] # previous solution
Gamma0 = 10 # DDRX decay-rate magnitude
M = Gamma0 * sf.M_DDRX(nlm_prev, S) # DDRX operator
nlm[tt,:] = nlm_prev + dt*np.matmul(M, nlm_prev) # euler step
nlm[tt,:] = sf.apply_bounds(nlm[tt,:]) # apply spectral bounds if needed