Continous dynamic recrystallization (CDRX)

Polygonization (rotation recrystallization, CDRX) accounts for the division of grains along internal sub-grain boundaries resulting from local strain incompatibilities. In effect, CDRX reduces the average grain size upon grain division but does not necessarily change the CPO much (Alley, 1992).

Following Gödert (2003), CDRX can be modeled by approximating this effect as a Laplacian diffusive process on \(S^2\):

\[ \frac{\mathrm{D} n}{\mathrm{D} t} = \Lambda\nabla^2 n , \]

where \(\Lambda\) is the CDRX rate-factor magnitude that depends on temperature, stress, strain-rate, etc. (Richards et al., 2021).

Limited use

Notice that this model is currently only relevant to slip-system normals. The model is therefore not yet useful for e.g. olivine.

Matrix model

The corresponding effect on the continuous distribution function is

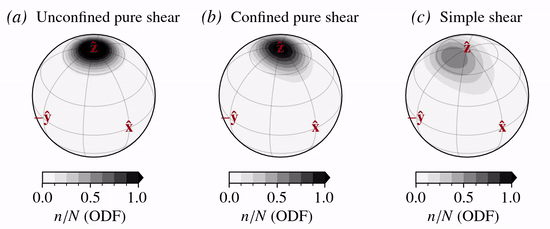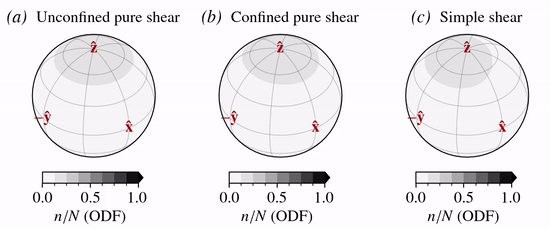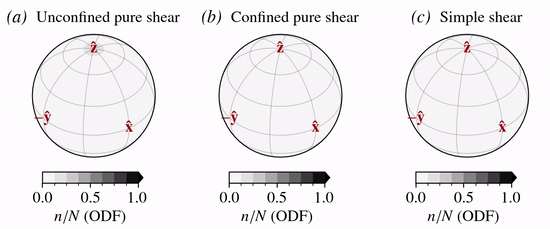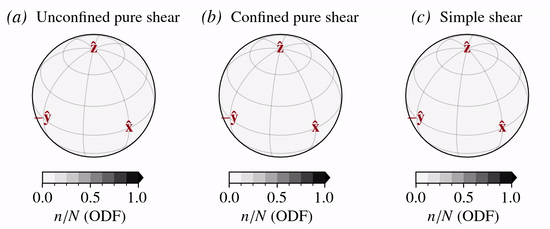
\[ \frac{\mathrm{D} n}{\mathrm{D} t} = \Lambda\nabla^2 n \quad\Longrightarrow\quad \frac{\mathrm{D} {\bf s}}{\mathrm{D} t} = {\bf M_{\mathrm{CDRX}}} \cdot {\bf s} . \]

Code example

import numpy as np
from specfabpy import specfab as sf
# L=8 truncation is sufficient in this case, but larger L allows a very strong fabric to  
#  develop and minimizes the effect that regularization has on low wavenumber modes (l=2,4)
lm, nlm_len = sf.init(8) 

### Velocity gradient tensor experienced by parcel

ugrad = np.diag([0.5, 0.5, -1.0]) # uniaxial compression along z-axis
D = (ugrad+np.transpose(ugrad))/2 # symmetric part (strain rate tensor)
W = (ugrad-np.transpose(ugrad))/2 # anti-symmetric part (spin tensor)

### Numerics 

Nt = 25   # number of time steps
dt = 0.05 # time-step size

### Initial fabric state

nlm = np.zeros((Nt,nlm_len), dtype=np.complex64) # n state vector
nlm[0,0] = 1/np.sqrt(4*np.pi) # normalized isotropic state at t=0

### Euler integration

for tt in np.arange(1,Nt):
    nlm_prev = nlm[tt-1,:] # previous solution
    Lambda = 1             # CDRX rate-factor
    M = Lambda*sf.M_CDRX(nlm) # CDRX operator 
    nlm[tt,:] = nlm_prev + dt*np.matmul(M, nlm_prev) # euler step
    nlm[tt,:] = sf.apply_bounds(nlm[tt,:]) # apply spectral bounds if needed