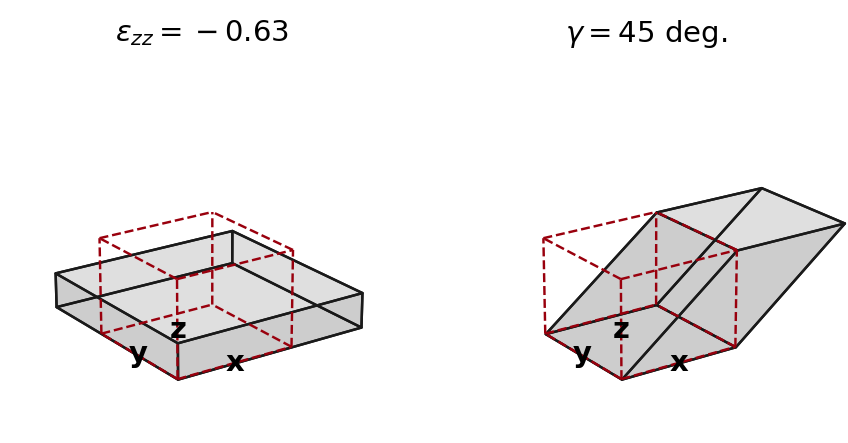
Plotting

CPO

The orientation distribution function (ODF; normalized expansion series) can be plotted as follows:

import numpy as np
import matplotlib.pyplot as plt
from specfabpy import specfab as sf
from specfabpy import plotting as sfplt
lm, nlm_len = sf.init(6)

### CPO to be plotted
a2 = np.diag([0,0,1]) # CPO characterized by a^(2)
nlm = sf.a2_to_nlm(a2) # vector of expansion coefficients

### Setup axes and projection
geo, prj = sfplt.getprojection(rotation=45, inclination=45)
fig = plt.figure(figsize=(2,2))
ax = plt.subplot(111, projection=prj)
ax.set_global() # ensure entire S^2 is shown

### Plot
lvlset = 'iso-up' # default level set: lowest tick/level is the value of an isotropic distribution
lvlset = (np.linspace(0,0.8,9), lambda x,p:'%.1f'%x) # custom level set: (list of levels, how to format colorbar tick labels)
sfplt.plotODF(nlm, lm, ax, cmap='Greys', lvlset=lvlset) # plot distribution (see src/specfabpy/plotting.py for API)
sfplt.plotcoordaxes(ax, geo, color=sfplt.c_dred) # plot coordinate axes (see src/specfabpy/plotting.py for API)
plt.savefig('ODF-plot.png', dpi=175, pad_inches=0.1, bbox_inches='tight')

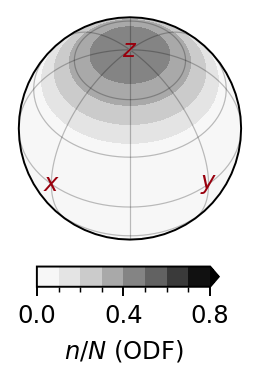
Parcel deformation

Given a deformation gradient \({\bf F}\), the effect on an undeformed parcel can be plotting following:

import numpy as np
import matplotlib.pyplot as plt
from specfabpy import specfab as sf
from specfabpy import plotting as sfplt
lm, nlm_len = sf.init(6)

### Determine deformation gradient F

# Pure shear 
axis = 2 # axis of compression/extension (0=x, 1=y, 2=z)
r    = 0 # deformation asymmetry
T_ps = 1 # e-folding time scale
t_ps = 1 # time at which deformed parcel is sought
F_ps = sf.pureshear_F(axis, r, T_ps, t_ps) # deformation gradient tensor 

# Simple shear
plane = 1 # shear plane (0=yz, 1=xz, 2=xy)
T_ss  = 1 # characteristic time taken to reach shear strain 45 deg.
t_ss  = 1 # time at which deformed parcel is sought
F_ss  = sf.simpleshear_F(plane, T_ss, t_ss) # deformation gradient tensor

### Plot
fig = plt.figure(figsize=(6,6))
ax1 = plt.subplot(121, projection='3d')
ax2 = plt.subplot(122, projection='3d')
sfplt.plotparcel(ax1, F_ps, azim=35, axscale=1.7, axislabels=True, drawinit=True)
sfplt.plotparcel(ax2, F_ss, azim=35, axscale=1.7, axislabels=True, drawinit=True)
ax1.set_title(r'$\epsilon_{zz}=%.2f$'%(sf.F_to_strain(F_ps)[2,2]))
ax2.set_title(r'$\gamma=%.0f$ deg.'%(np.rad2deg(sf.simpleshear_gamma(T_ss, t_ss))))
plt.savefig('deformed-parcel.png', dpi=175, pad_inches=0.1, bbox_inches='tight')