Plastic spin

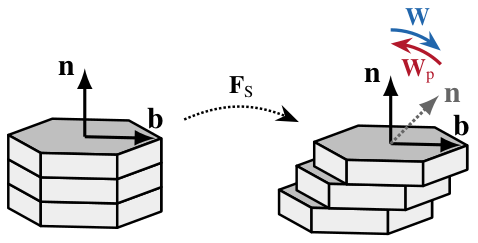
When subject to simple shear, the orientation of easy slip systems in polycrystalline materials like ice or olivine tend towards aligning with the bulk shear-plane system. That is, the \(n\)-axis (\(c\)-axis in ice) tends towards to bulk shear plane normal, and the \(b\)-axis (\(a\)-axis in ice) towards to bulk shear direction. Thus, if grains are perfectly aligned with the bulk shear system, their orientation should be unaffected by any further shearing, but be in steady state. Clearly, slip systems do therefore not simply co-rotate with the bulk continuum spin (\(\bf W\)) like passive material line elements embedded in a flow field, i.e. \({\bf \dot{n}} \neq {\bf W} \cdot {\bf n}\). Rather, slip systems must be subject to an additional contribution — a plastic spin \({\bf W}_\mathrm{p}\) — such that the bulk spin is exactly counteracted to achieve steady state if favourably aligned:

\[ {\bf \dot{n}} = ({\bf W} + {\bf W}_{\mathrm{p}}) \cdot {\bf n} = {\bf 0} \quad\text{for ${\bf b}$–${\bf n}$ shear}. \]

Here, the functional form of \({\bf W}_\mathrm{p}\) is breifly discussed following Aravas and Aifantis (1991) and Aravas (1994) (among others).

For a constant rate of shear deformation (\(1/T\)) aligned with the \({\bf b}\)—\({\bf n}\) system,

\[ {\bf F}_{\mathrm{S}} = {\bf I} + \frac{t}{T} {\bf b}\otimes{\bf n} \quad \Rightarrow\quad \nabla {\bf u} = \frac{1}{T} {\bf b}\otimes{\bf n} , \]

the bulk strain-rate and spin tensors are, respectively,

\[ {\bf D} = \frac{1}{2T} ({\bf b}\otimes{\bf n} + {\bf n}\otimes{\bf b}), \\ {\bf W} = \frac{1}{2T} ({\bf b}\otimes{\bf n} - {\bf n}\otimes{\bf b}) . \]

Since \({\bf W}_\mathrm{p} = -{\bf W}\) is required in steady state, it follows from eliminating \(1/(2T)\) by calculating \({\bf D} \cdot {\bf n}\otimes{\bf n}\), \({\bf n}\otimes{\bf n} \cdot {\bf D}\), \({\bf D} \cdot {\bf b}\otimes{\bf b}\), and \({\bf b}\otimes{\bf b} \cdot {\bf D}\), that

\[ {\bf W}_\mathrm{p}({\bf D},{\bf n}) = +{\bf n}\otimes{\bf n} \cdot {\bf D} - {\bf D} \cdot {\bf n}\otimes{\bf n} , \\ {\bf W}_\mathrm{p}({\bf D},{\bf b}) = -{\bf b}\otimes{\bf b} \cdot {\bf D} + {\bf D} \cdot {\bf b}\otimes{\bf b} , \]

so that

\[ {\bf \dot{n}} = ({\bf W} + {\bf W}_{\mathrm{p}}({\bf D},{\bf n})) \cdot {\bf n}, \\ {\bf \dot{b}} = ({\bf W} + {\bf W}_{\mathrm{p}}({\bf D},{\bf b})) \cdot {\bf b}. \]

Indeed, this result agrees with representation theorems for isotropic functions (Wang, 1969), stating that an anti-symmetric tensor-value function of a symmetric tensor (\({\bf D}\)) and a vector (\({\hat {\bf r}}\)) is to lowest order given by

\[ {\bf W}_{\mathrm{p}}({\bf D},{\hat {\bf r}}) = \iota({\hat {\bf r}}\otimes{\hat {\bf r}}\cdot{\bf D} - {\bf D}\cdot{\hat {\bf r}}\otimes{\hat {\bf r}}) . \]

To be consistent with the above, \(\iota = +1\) for \({\hat {\bf r}}={\bf n}\) and \(\iota = -1\) for \({\hat {\bf r}}={\bf b}\).

\({\bf W}_\mathrm{p}({\bf D},{\bf n})\) and \({\bf W}_\mathrm{p}({\bf D},{\bf b})\) are then generally taken to relevant for other modes of deformation, too.