Regularization
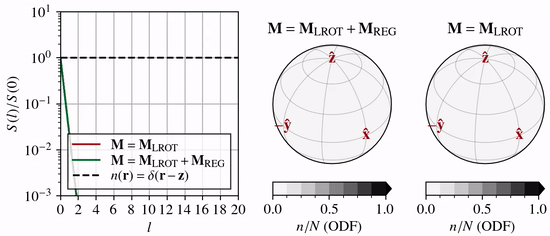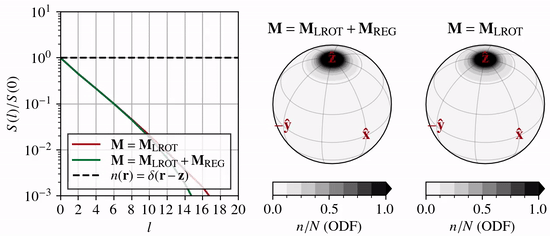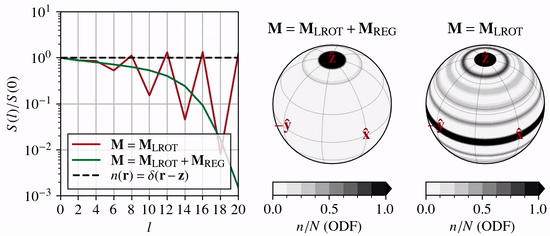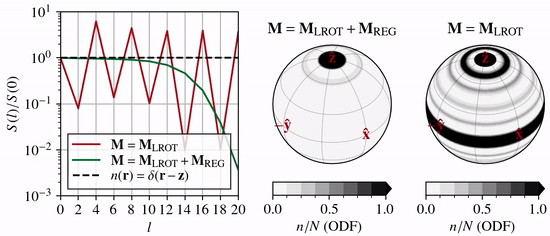
As \(n(\theta,\phi)\) and \(b(\theta,\phi)\) becomes anisotropic due to CPO processes, the coefficients \(n_l^m\) and \(b_l^m\) associated with high wavenumber modes (large \(l\) and \(m\), and thus small-scale structure) must increase in magnitude relative to the low wavenumber coefficients (small \(l\) and \(m\)).
One way to visualize this is by the angular power spectrum (and similarly for \(b(\theta,\phi)\))
which grows with time. In the animation above, the left-hand panel shows how the power spectrum evolves under lattice rotation (unconfined vertical compression) compared to the end-member case of a delta function (dashed line).
If the expansion series is truncated at \(l=L\), then \(l{\gt}L\) modes cannot evolve, and the truncated solution will reach an unphysical quasi-steady state. To prevent this, regularization must be introduced. Specfab uses Laplacian hyper diffusion (\(k>1\)) as regularization in \(S^2\)
that can be added to the fabric evolution operator \({\bf M}\) as follows:
M += sf.M_REG(nlm, D) # D = strainrate tensor
This allows the growth of high wavenumber modes to be disproportionately damped (green line compared to red line in animation above). The dependency on the strain-rate tensor guarantees the same behavior irrespective of strain rate magnitude.
Strength of regularization
Extra spectral width
As a rule-of-thumb, regularization affects the highest (\(l=L\)) and next-highest (\(l=L-2\)) harmonics and can therefore not be expected to evolve freely. This, in turn, means that the structure tensors \({\bf a}^{(2)}\) and \({\bf a}^{(4)}\), and hence derived enhancement factors, might be affected by regularization unless extra spectral width is dedicated by setting \(L{\geq}8\).