CPO dynamics for orthotropic grains

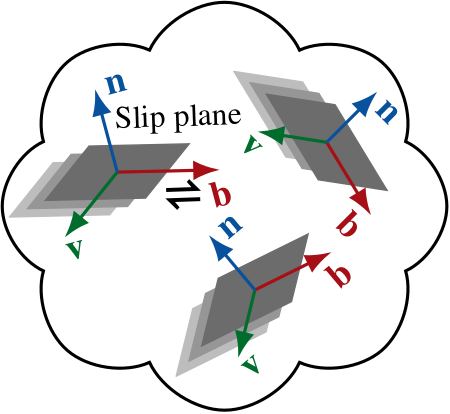
This tutorial focuses on modelling the CPO evolution of polycrystalline olivine. That is, the distribution of (easy) slip-plane normals and slip directions of grains, $n(\theta,\phi)$ and $b(\theta,\phi)$.

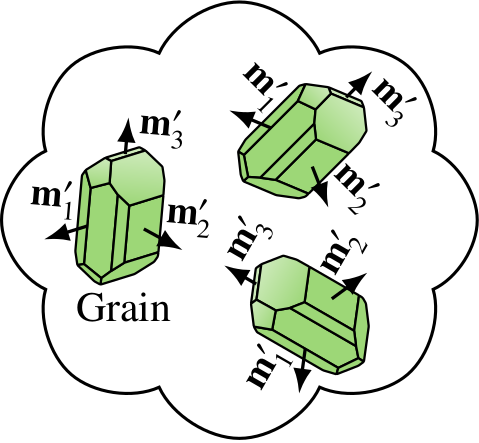
Polycrystalline olivine	Ensemble of slip elements

The distributions $n(\theta,\phi)$ and $b(\theta,\phi)$ refer to certain crystallographic axes (${\bf m}'_i$) depending on the fabric type; i.e. thermodynamic conditions, water content, and stress magnitude that control which of the crystallographic slip systems is activated.

Problem

Given the expansions

\[ n({\bf x},t,\theta,\phi)=\sum_{l=0}^{L}\sum_{m=-l}^{l}n_{l}^{m}({\bf x},t) Y_{l}^{m}(\theta,\phi) \quad\text{(distribution of slip-plane normals)}, \\ b({\bf x},t,\theta,\phi)=\sum_{l=0}^{L}\sum_{m=-l}^{l}b_{l}^{m}({\bf x},t) Y_{l}^{m}(\theta,\phi) \quad\text{(distribution of slip directions)}, \]

CPO evolution can be written as two independent matrix problems involving the CPO state vector fields

\[ {\bf s}_n = [n_0^0,n_2^{-2},n_2^{-1},n_2^{0},n_2^{1},n_2^{2},n_4^{-4},\cdots,n_4^{4},\cdots,n_L^{-L},\cdots,n_L^{L}]^{\mathrm{T}} \quad\text{($n$ state vector)}, \\ {\bf s}_b = [b_0^0,b_2^{-2},b_2^{-1},b_2^{0},b_2^{1},b_2^{2},b_4^{-4},\cdots,b_4^{4},\cdots,b_L^{-L},\cdots,b_L^{L}]^{\mathrm{T}} \quad\text{($b$ state vector)}, \]

such that

\[ \frac{\mathrm{D}{\bf s}_n}{\mathrm{D} t} = {\bf M}_n \cdot {\bf s}_n \quad\text{($n$ state evolution)}, \\ \frac{\mathrm{D}{\bf s}_b}{\mathrm{D} t} = {\bf M}_b \cdot {\bf s}_b \quad\text{($b$ state evolution)}, \]

where the operators (matrices) ${\bf M}_n$ and ${\bf M}_b$ represents the effect of a given CPO process, which may depend on stress, strain-rate, temperature, etc.

Note

The distributions may also be understood as the mass density fraction of grains with a given slip-plane-normal and slip-direction orientation. See CPO representation for details.

Lagrangian parcel

The tutorial shows how to model the CPO evolution of a Lagrangian material parcel subject to three different modes of deformation:

Lattice rotation

To be published before documented here.

Regularization

Same as CPO dynamics for transversely isotropic grains