Elastic constitutive equations
Linear elastic constituve equations are supported in both forward and inverse (reverse) form.
Transversely isotropic
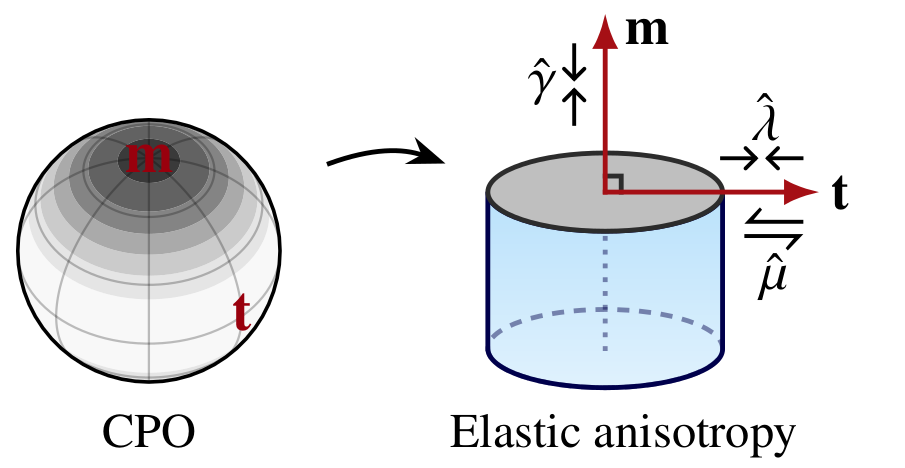
The stiffness matrix is for the special case \({\bf c}=\hat{{\bf z}}\) (allowing easy interpretation):
\[
{\bf C} = \begin{bmatrix}\gamma & \lambda & \hat{\lambda}\lambda & 0 & 0 & 0 \\\lambda & \gamma & \hat{\lambda}\lambda & 0 & 0 & 0 \\\hat{\lambda}\lambda & \hat{\lambda}\lambda & \hat{\gamma}\gamma & 0 & 0 & 0 \\0&0&0& \hat{\mu}\mu & 0 & 0\\0&0&0& 0 & \hat{\mu}\mu & 0\\0&0&0& 0 & 0 & \mu\\\end{bmatrix}
.
\]
API
- Forward form:
E = sf.elas_fwd_tranisotropic(S, lam, mu, Elam, Emu, Egam, m) - Inverse form:
S = sf.elas_rev_tranisotropic(E, lam, mu, Elam, Emu, Egam, m)
| Arguments | Description |
|---|---|
S, E |
Stress and strain tensor (3x3) |
lam, mu |
Isotropic Lamé parameters \(\lambda\) and \(\mu\) |
Elam, Emu, Egam |
Anisotropic enhancement factors \(\hat{\lambda}\), \(\hat{\mu}\), and \(\hat{\gamma}\) |
m |
Rotational symmetry axis \(\bf{m}\) |
Notice: P-wave modulus is not a free parameter but given by \(\gamma \equiv \lambda + 2\mu\).
Tip: convert \(C_{ij}\) to Lamé parameters
Cij = (C11,C33,C55, C12,C13)
(lam,mu, Elam,Emu,Egam) = sf.Cij_to_Lame_tranisotropic(Cij)
Orthotropic
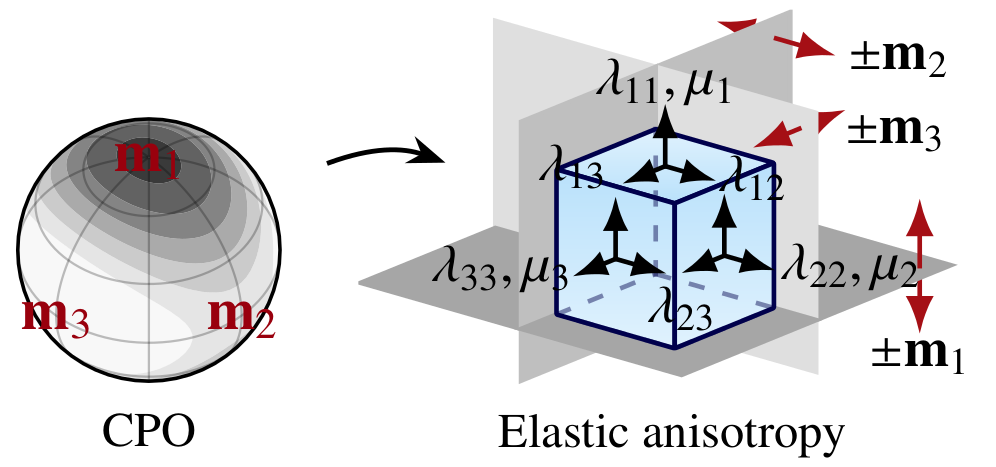
The stiffness matrix is for the special case \(({\bf m}_1,{\bf m}_2,{\bf m}_3)=(\hat{{\bf x}},\hat{{\bf y}},\hat{{\bf z}})\) (allowing easy interpretation):
\[
{\bf C} = \small\begin{bmatrix} \lambda_{11} + 2\mu_1 & \lambda_{12} & \lambda_{13} & 0 & 0 & 0 \\ \lambda_{12} & \lambda_{22} + 2\mu_2 & \lambda_{23} & 0 & 0 & 0 \\ \lambda_{13 }& \lambda_{23} & \lambda_{33} + 2\mu_3 & 0 & 0 & 0 \\ 0 & 0 & 0 & \dfrac{\mu_2+\mu_3}{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \dfrac{\mu_3+\mu_1}{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \dfrac{\mu_1+\mu_2}{2} \end{bmatrix}
.
\]
API
- Forward form:
E = sf.elas_fwd_orthotropic(S, lame, m1,m2,m3) - Inverse form:
S = sf.elas_rev_orthotropic(E, lame, m1,m2,m3)
| Arguments | Description |
|---|---|
S, E |
Stress and strain tensor (3x3) |
lame |
Tuple of anisotropic Lamé parameters \((\lambda_{11},\lambda_{22},\lambda_{33}, \lambda_{23},\lambda_{13},\lambda_{12}, \mu_{1}, \mu_{2}, \mu_{3})\) |
m1, m2, m3 |
Reflection symmetry axes \(\bf{m}_1\), \(\bf{m}_2\), and \(\bf{m}_3\) |
Tip: convert \(C_{ij}\) to Lamé parameters
Cij = (C11,C22,C33,C44,C55,C66, C23,C13,C12)
(lam11,lam22,lam33, lam23,lam13,lam12, mu1,mu2,mu3) = sf.Cij_to_Lame_orthotropic(Cij)